Επιστήμη
Η Θεωρία του Χάους
Στο άρθρο παρουσιάζεται η θεωρία του Χάους εκλαϊκευμένη και στοιχεία της επίδρασής της στην καθημερινή μας πράξη. Δίνεται ιδιαίτερη σημασία στην επίδραση των θεωριών του χάους στην καλλιτεχνική έκφραση γιατί είναι σχεδόν πάντα ο φανερός πρόσκοπος των εξελικτικών βημάτων κάθε κοινωνίας. Τέλος εκτίθονται σκέψεις για το ποια μπορεί να είναι η μεταμορφωτική και εξελικτική επίδραση των θεωριών του Χάους στην συνείδηση.
Χάος
Και λοιπόν πρώτα από όλα το Χάος γεννήθηκε και μετά
η πλατύστερνη Γαία, η αιώνια και ασφαλής έδρα των πάντων
και ο σκοτεινός Τάρταρος
σε μια τρύπα στα έγκατα της απλωμένης γης
και ο Έρως, ο πιο όμορφος ανάμεσα στους Αθάνατους Θεούς
που τα μέλη παραλύει σε Θεούς και σε ανθρώπους
που υποτάσσει τα στήθη, το μυαλό και τη σύνεση[1].
…μας λέει ο Ησίοδος στην Θεογονία: «Πριν από κάθε άλλο ήταν το Χάος».
Εισαγωγή
Μα τι ήτανε το χάος κατά τον Ησίοδο; Ήταν ο Χώρος: ένας χώρος που περιείχε εν σπέρματι όλα όσα θα αποτελέσουν το Σύμπαν…Επομένως το Χάος είναι η αρχή όλων των πραγμάτων, γέννησε το έρεβος και την νύχτα χωρίς καμία βοήθεια. Το χάος είναι λοιπόν η κύρια και δημιουργός αρχή[2].
Βεβαίως και δεν είναι τυχαία η επιλογή της λέξης χάος για την φυσική θεωρία που περιγράφει φαινόμενα πολύ ευαίσθητα στην επίδραση ασήμαντων αρχικών συνθηκών.
Στον αιώνα που πέρασε έγιναν τρεις μεγάλες επιστημονικές επαναστάσεις: η θεωρία της σχετικότητας που διεύρυνε την αντίληψή μας για τον χωρόχρονο, η κβαντική μηχανική που εμβάθυνε στην αρχή της αιτιότητας θεμελιώνοντάς την για τον μικρόκοσμο και η θεωρία του Χάους που ανιχνεύει τα όρια του αιτιατού και του τυχαίου.
Στην επιστήμη το χάος χρησιμοποιείται για να περιγράψει την συμπεριφορά συστημάτων με εξαιρετικά ευαίσθητη εξάρτηση από τις αρχικές τους συνθήκες. Η ανεξέλεγκτη, απειροελάχιστη μεταβολή στις αρχικές συνθήκες εκδηλώνεται ως χάος-αταξία, αδυναμία πρόβλεψης σε μια κατά τα άλλα αναμενόμενη τακτική και σταθερή φυσική διαδικασία.
Τα σύστημα αυτά, οδηγούνται από έναν «ελκυστή», σε μία κατάσταση που παρουσιάζει μεν μια σταθερότητα στην συμπεριφορά της όμως η πρόβλεψη της είναι αδύνατον να εκφραστεί με αιώνιους νόμους ή ντερμινιστικά.
Ένα χαρακτηριστικό παράδειγμα είναι μια τυχαία μορφή που δημιουργείται κατά την ροή ενός ποταμού: η μικρή δύνη μετά από μια πέτρα. Η πέτρα είναι ο ελκυστής, η ροή που έρχεται καθορίζει τις αρχικές συνθήκες, όμως για την δύνη, δεν μπορεί να προβλεφθεί η ακριβής της μορφή. Είναι εκεί, όμως το σχήμα αλλάζει διαρκώς, μερικές φορές μοιάζει να χάνεται, άλλοτε να γίνεται κανονικό, όμως δεν μπορεί να προβλεφθεί ντετερμινιστικά ανά πάσα στιγμή. Την υποτυπώδη αυτή γεωμετρική μορφή οι μαθηματικοί του χάους ονομάζουν παράξενο ελκυστή.
Τα παραδείγματα είναι πολλά: Ο καπνός του τσιγάρου που στροβιλίζεται ανεβαίνοντας. Η ροή του νερού που τρέχει από μια βρύση. Το σχήμα των κυμάτων σε μια ακτή. Ο τρόπος που το μελάνι που διαχέεται σε ένα ποτήρι νερού. Η τυχαία μεταβολή κάποιας ιδιότητας, π.χ. κλίση τροχιάς, εκκεντρότητας τροχιάς ενός πλανήτη.
Στη βιολογία, στην κοινωνιολογία, στην οικονομία και στην ιατρική υπάρχουν παρόμοιες εκδηλώσεις χαοτικής συμπεριφοράς.
Τα παραδείγματα δεν τελειώνουν εδώ. Χαοτικά συστήματα υπάρχουν παντού. Το απρόβλεπτο των τιμών στο χρηματιστήριο, στα ηλεκτρικά κυκλώματα, στους χτύπους της καρδιάς, στην ροή του νερού ή του αίματος μέσα στους σωλήνες, στην μεταβολή των πληθυσμών στα πουλιά και στα φυτά είναι ορισμένοι τομείς στους οποίους ενυπάρχει το χάος.
Στην δεκαετία του 1970 οι επιστήμονες άρχισαν να προσεγγίζουν την έννοια της αταξίας, με σκοπό να γνωρίσουν τις νομοτέλειές της. Διαπίστωσαν ότι τα ανεξέλεγκτα αυτά φαινόμενα, μπορούν κατά κάποιο τρόπο να περιγραφούν με μη-γραμμικές εξισώσεις. Έτσι άρχισε να αποκαλύπτεται μια κρυφή τάξη που τα ορίζει, να δημιουργούνται οι προϋποθέσεις ώστε να μπορούν να διατυπωθούν προβλέψεις.
Βέβαια η προσέγγιση τέτοιων συστημάτων, ο τρόπος που πρέπει να σταθεί κανείς απέναντί τους για να προβλέψει την εξέλιξή τους και για να καθορίσει την έκβασή τους, προϋποθέτει αναδιαμόρφωση της νοοτροπίας του. Όπως άλλωστε συμβαίνει σε κάθε έναν που διδάσκεται.
Η Αναγκαιότητα Δημιούργησε την Θεωρία του Χάους
Μέχρι τα τέλη του προ-περασμένου αιώνα η τροχιά κάθε ουράνιου σώματος που θεωρούνταν περιοδική και κανονική σαν τη κίνηση ενός τέλειου εκκρεμούς, υπολογιζόταν με τη βοήθεια των νόμων του Νεύτωνα και του Κέπλερ[3].
Ήταν τέλη του 19ου αιώνα, όταν ο μαθηματικός και αστρονόμος Henri Poincare, διαπίστωσε ότι το πρόβλημα συσχετισμού της κίνησης των τριών σωμάτων Ήλιου, Γης και Σελήνης ήταν και παραμένει άλυτο. Ότι δεν μπορεί να προβλεφθεί η τροχιά οποιουδήποτε ουράνιου σώματος που δέχεται την επίδραση δύο η περισσοτέρων άλλων σωμάτων. Η προσπάθεια λοιπόν να υπολογιστεί η τροχιά πχ του Πλούτωνα, δεν είναι δυνατή, αφού δέχεται την επίδραση του Ήλιου και άλλων οκτώ πλανητών.
Ο Poincare αποκάλυψε το χάος στο Ηλιακό σύστημα. Είχε κατανοήσει πως πολύ μικρές επιδράσεις μπορούν να μεγεθυνθούν μέσω ανάδρασης. Διατύπωσε την άποψη «Μια ελάχιστη αιτία που διαφεύγει της προσοχής μπορεί να προκαλέσει ένα σημαντικό αποτέλεσμα».
Χρειάστηκε να περάσουν 80 χρόνια από τότε για να συνειδητοποιήσουν οι αστρονόμοι και οι υπόλοιποι επιστήμονες τη σπουδαιότητα αυτής της ανακάλυψης. Το 1954 πρώτος την κατανόησε ο σοβιετικός επιστήμονας A.Kolmogorov και ακολούθησαν και άλλοι.
Στα μέσα του χειμώνα 1961, ο μετεωρολόγος Edward Lorenz εργαζόταν στον υπολογιστή του ΜΙΤ και διαπίστωσε ότι η επανάληψη (iteration) γεννά το χάος. Για να λύσει μη γραμμικές εξισώσεις που περιέγραφαν το μοντέλο της γήινης ατμόσφαιρας, έδωσε δεδομένα με στρογγυλοποιημένους αριθμούς. Ενώ περίμενε την ίδια περίπου πρόγνωση όπως με τους δεκαδικούς αριθμούς, τα νέα αποτελέσματα ήταν τελείως διαφορετικά. Κατάλαβε πως η μεγέθυνση των διαφορών οφείλεται στο συνδυασμό της μη γραμμικότητας και της επανάληψης.
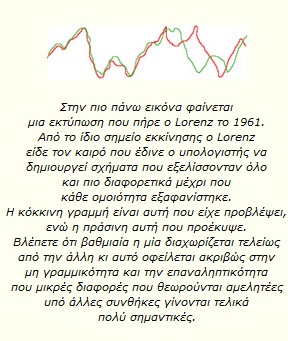 Στον Lorenz οφείλεται η θεωρία για την πεταλούδα που πετάει στο Χονγκ-Κονγκ και μπορεί να δημιουργήσει καταιγίδα στη Νέα Υόρκη.
Στον Lorenz οφείλεται η θεωρία για την πεταλούδα που πετάει στο Χονγκ-Κονγκ και μπορεί να δημιουργήσει καταιγίδα στη Νέα Υόρκη.
Ξαφνικά οι επιστήμονες συνειδητοποίησαν πως σε αιτιοκρατικά δυναμικά συστήματα, η δυνατότητα γέννησης χάους (μη προβλεψιμότητας) παραμονεύει σε κάθε λεπτομέρεια. ΄Aρχισαν λοιπόν να μελετούν το χάος στην εφαρμοσμένη επιστήμη. Έτσι βρέθηκε μια εκπληκτική τάξη στο χάος που αναπτύσσεται στην ανθρώπινη καρδιά, την κύρια αιτία του απρόσμενου θανάτου. Ερευνήθηκε η εμφάνιση και εξαφάνιση νομαδικών πληθυσμών εντόμων. Εξετάστηκαν οι τιμές προϊόντων συναρτήσει επιρροών που φαίνονται μηδαμινές. Εξετάστηκε το σχήμα των νεφών, οι διαδρομές των αστραπών στον αέρα. Ερευνήθηκε η ομαδοποίηση των άστρων σε γαλαξίες. Και η εφαρμογή του συνεχώς διευρύνεται από την διαστημική έως τη δυναμική των υγρών, τις ακτίνες laser έως τις χημικές αντιδράσεις, από τις τηλεπικοινωνίες (λευκός θόρυβος της γραμμής) έως την νευροφυσιολογία. Αλλά τελευταία ενδιαφέρει τους μουσικούς, τους συγγραφείς, τους ψυχαναλυτές τους εικαστικούς κοκ.
Η ονομασία Θεωρία του Χάους δόθηκε από τον μαθηματικό του Πανεπιστημίου του Maryland Jim York μόλις το 1975.
Η θεωρία του χάους έχει ένα σημαντικό και εξαιρετικά δυσνόητο μαθηματικό φορμαλισμό. Υπάρχει ο ισχυρισμός ότι δεν είναι μια ενοποιημένη θεωρία, αλλά μια μαθηματική πλατφόρμα πάνω στην οποία μπορούν να αναπτυχθούν ερμηνείες φαινομένων. Στα πρώτα βήματα, για να ανοίξει κανείς μια χαραμάδα στην πόρτα που κρύβει πίσω της όλο το μαθηματικό σύμπαν της θεωρίας του χάους υπάρχουν κάποιες απλές μα σημαντικές έννοιες που είναι απαραίτητες στο λεξιλόγιο καθενός που θέλει να μιλήσει σχετικά. Τα βασικά συστατικά του μαθηματικού χώρου που χρησιμοποιεί η θεωρία του χάους είναι οι αναπαραστάσεις φαινομένων σε πολυδιάστατους χώρους, η μη γραμμική συμπεριφορά, η αναδρομή και η επαναληπτικότητα. Σημαντική μαθηματική οντότητα της περιγραφής των χαοτικών συστημάτων είναι οι παράξενοι ελκυστές. Αλλά τι είναι όλα αυτά;
Ορισμοί
Μη Γραμμικά Συστήματα
Γραμμικά θεωρούνται τα συστήματα για τα οποία ισχύει το άθροισμα δύο λύσεων τους είναι κι αυτό λύση. Όταν λέμε λύση ενός συστήματος μπορούμε απλοποιημένα να θεωρήσουμε πως εννοούμε την δυνατότητα να γνωρίζουμε σε κάποιο καθορισμένο χρόνο την κατάσταση του συστήματος. Αν για παράδειγμα έχουμε δύο λύσεις την λύση χ=5 και την χ=3, τότε για τα γραμμικά συστήματα και η λύση 5+3=8 είναι λύση. Αυτή η ιδιότητα των γραμμικών συστημάτων τα απλουστεύει πολύ. Στα μη γραμμικά αυτό δεν συμβαίνει. Τα μη γραμμικά συστήματα είναι εξαιρετικά πιο δύσκολο να λυθούν.
Διαστάσεις
Οι διάφορες παράμετροι της συμπεριφοράς του εκκρεμούς μπορούν να οριστούν σαν διαστάσεις. Υπάρχουν τουλάχιστον τέσσερις, οι τρεις του χώρου (x,y,z) και ο χρόνος. Αν το ίδιο το εκκρεμές είναι παγάκι που λιώνει, τότε το βάρος του θα αλλάζει διαρκώς. Το βάρος αφού αλλάζει μπορούμε να το θεωρήσουμε μια επιπλέον διάσταση, η πέμπτη διάσταση. Η συμπεριφορά ενός συστήματος περιγράφεται σαν μια τροχιά που διαγράφεται σε αυτόν τον ιδεατό πενταδιάστατο χώρο.
Όσο περισσότερες είναι οι παράμετροι που αλλάζουν σε ένα σύστημα που παρατηρούμε τόσο περισσότερες είναι και οι διαστάσεις του χώρου που χρειαζόμαστε για το αναπαραστήσουμε μαθηματικά.
Αναδρομή
Κάθε σύστημα χαρακτηρίζεται από είσοδο, διαδικασία και έξοδο.
Για παράδειγμα στην κίνηση του εκκρεμούς είσοδος είναι η χρονική στιγμή t για την οποία θέλουμε να μάθουμε ποια είναι η θέση του x. Έξοδος είναι η θέση x του εκκρεμούς. Διαδικασία είναι η εξίσωση της ταλάντωσης που περιγράφει μαθηματικά τον τρόπο που η είσοδος καθορίζει την έξοδο. x=Aημωt
 Επαναληπτικότητα
Επαναληπτικότητα
Είναι ένα χαρακτηριστικό των εξισώσεων του χάους. Για να λάβουμε τα δεδομένα εξόδου τους είναι απαραίτητο η διαδικασία να επαναληφθεί πολλές φορές. Αυτό σχετίζεται με την ανάδραση, διότι για να αντιληφθώ σε τι κατάσταση βρίσκεται ένα σύστημα μετά την τρίτη επανάληψη χρειάζομαι τα αποτελέσματα της προηγούμενης δηλαδή της δεύτερης. Για παράδειγμα αν έχω ένα ζευγάρι που γνωρίζω ότι δίνει δύο απογόνους σε κάθε γενιά, μετά από τρεις γενιές πως θα υπολογίσω τον συνολικό πληθυσμό όταν κάθε ζευγάρι δίνει δύο απογόνους;
Χρειάζεται να επαναλάβω την διαδικασία τρεις φορές. Μια για κάθε γενιά:
(Α γενιά) = (2+2)
(Β γενιά) = (Α γενιά) + (πλήθος ζευγαριών)*2 = [(2+2) + ((2+2)/2) * 2]
(Γ γενιά) = (Β γενιά) + (πλήθος ζευγαριών) * 2 = [(2+2) + ((2+2)/2) * 2] + {[(2+2) + ((2+2)/2) * 2]/2} * 2
Ο γενικός κανόνας λοιπόν είναι:
(Ν γενιά) = ([Ν-1] γενιά) + {[([Ν-1] γενιά)/2] * 2} = 2 * ([Ν-1] γενιά) δηλαδή
(Ν γενιά) = 2 * ([Ν-1] γενιά).
Στο παράδειγμα αυτό φαίνεται και η έννοια των αρχικών συνθηκών που εδώ είναι ένα ζευγάρι. Κάθε άλλο πλήθος ζευγαριών είναι και μια άλλη αρχική συνθήκη.
Παράξενοι ελκυστές
Ας πάρουμε για αρχή την κίνηση ενός ιδανικού εκκρεμούς. Μετά από μια ώθηση, παλινδρομεί μέχρι να ηρεμήσει και πάλι στο κέντρο. Η κεντρική αυτή θέση είναι το σημείο έλξης του συστήματος. Σε όποια θέση και αν αφήσουμε το εκκρεμές, θα έλκεται από αυτό το σημείο που ονομάζεται ελκυστής. Στην κλασική λοιπόν μηχανική, η συμπεριφορά ενός δυναμικού συστήματος μπορεί να περιγραφεί γεωμετρικά ως κίνηση προς έναν ελκυστή. Οι ελκυστές μπορεί να είναι σημεία, καμπύλες, στερεά που ακριβώς έλκουν ένα συγκεκριμένο φαινόμενο. Σε ένα ταλαντούμενο σώμα ο ελκυστής είναι το κατώτατο σημείο που σταματάει.
Αντίθετα με το απλό παράδειγμα του ιδανικού εκκρεμούς, τα χαοτικά συστήματα έλκονται προς παράξενα και πολύπλοκα σχήματα. Αυτό είναι σχεδόν αδύνατο να το αντιληφθούμε, δεδομένου ότι αναφερόμαστε σε πολυδιάστατους χώρους για να προσδιορίσουμε τους ελκυστές. Οι ελκυστές των χαοτικών συστημάτων ονομάζονται παράξενοι ελκυστές και είναι οι χώροι από τους οποίους τείνει να λαμβάνει τιμές μια χαοτική συμπεριφορά. Μπορούμε να αντιληφθούμε σε μερικές μόνο περιπτώσεις με τα μάτια ένα αποτύπωμα, μια σκιά των παράξενων ελκυστών στον πραγματικό χωρόχρονο. Για παράδειγμα το σχήμα μιας δίνης στο νερό είναι η εξέλιξη ενός παράξενου ελκυστή στον χρόνο.
Οι παρακάτω είναι οι εξισώσεις του Lorentz:
x' = 3(y – x)
y' = -xz + 26.5x – y
z' = xy – z
οι οποίες με ελάχιστα μικρή απόκλιση στις αρχικές τιμές δημιουργούν χαοτική συμπεριφορά. Όμως αυτή η συμπεριφορά έχει έναν εσωτερικό κανόνα που φαίνεται στο γράφημα του παράξενου ελκυστή του Lorentz:
οποίες με ελάχιστα μικρή απόκλιση στις αρχικές τιμές δημιουργούν χαοτική συμπεριφορά. Όμως αυτή η συμπεριφορά έχει έναν εσωτερικό κανόνα που φαίνεται στο γράφημα του παράξενου ελκυστή του Lorentz:
Επειδή το σύστημα δεν παίρνει πoτέ τις ίδιες τιμές δύο φορές, η τροχιά δεν τέμνει τον εαυτό της ποτέ, αλλά δημιουργεί βρόχους επ' αόριστον. Η απεικόνιση αυτή εμφανίζει ένα είδος άπειρης πολυπλοκότητας. Η μορφή αυτή μοιάζει σαν δύο φτερά μιας πεταλούδας ή σαν ένα είδος διπλής έλικας. Το σχήμα φανερώνει μια καθαρή αταξία, αφού δεν εμφανίζονται ποτέ δύο ίδιες λύσεις αλλά και ένα νέο είδος τάξης αφού προκύπτεί ένα συγκεκριμένο σχήμα με μια συγκεκριμένη νομοτέλεια.
Γύρω στο 1960 ανακαλύφθηκε από τον μαθηματικό Stephen Smale μια νέα τάξη παράξενων ελκυστών για τους οποίους διαπιστώθηκε ότι έχουν λεπτομερή δομή σε όλες τις κλίμακες μεγέθυνσης. Παρουσιάζουν δηλαδή αυτοομοιότητα. Σε αυτούς τους ελκυστές δόθηκε η ονομασία fractal.
Φράκταλ: η Γεωμετρία της Θεωρίας του Χάους
Ο όρος fractal πλάσθηκε από μαθηματικό Benoit Β. Mandelbrot από την λατινική λέξη fractus (θρυμματισμένος ή σπασμένος), για να εκφράσει την ιδέα ενός σχήματος που οι διαστάσεις που χρειάζεται για να αναπαρασταθεί δεν είναι ακέραιος αριθμός και αναπαριστά συναρτήσεις από τα μαθηματικά του χάους. Στα Ελληνικά αποδόθηκε με τον όρο Μορφοκλασματική Καμπύλη από τον καθηγητές Στ. Πνευματικό και Ι. Νίκολη.
Οι υπολογιστές έδωσαν την δυνατότητα να αναπαρασταθούν γραφικά συναρτήσεις και παράξενοι ελκυστές που συναντά κανείς στα μαθηματικά της επιστήμης του χάους. Η πολυπλοκότητα των γραφικών αυτών αναπαραστάσεων απαιτεί σημαντική υπολογιστική ισχύ, παρόλο που τα προγράμματα είναι σχετικά απλά αφού βασίζονται στην επαναληπτικότητα των αλγορίθμων.
Συνήθως όταν ακούμε σχέδια ή σχήματα που προέρχονται από μαθηματικές συναρτήσεις έρχονται στο μυαλό μας κάποια ευκλείδεια γεωμετρικά σχήματα. Τα fractals διαφέρουν από αυτά τα σχήματα τον κύκλο, την έλλειψη το τετράγωνο κλπ. Η λέξη εικόνα σε αντίθεση με την λέξη σχήμα με αυτή την έννοια είναι μάλλον πιο κατάλληλη για να προσδιορίσει τις γραφικές αυτές αναπαραστάσεις[4].
Αυτοομοιότητα
Έ να χαρακτηριστικό τους ότι είναι όμοια προς εαυτόν. Έτσι αν κοιτάξουμε ένα μικρό τμήμα ενός fractal θα δούμε πως είναι όμοιο με ένα μεγαλύτερο τμήμα. Αν μεγεθύνουμε το μικρό, θα δούμε πως αυτό περιέχει και πάλι όμοια μέρη κ.ο.κ. Αυτή τους η ιδιότητα ονομάζεται αυτοομοιότητα. Αυτοόμοιο είναι ένα αντικείμενο του οποίου τα μέρη από τα οποία αποτελείται μοιάζουν με το σύνολο. Αυτή η επανάληψη των ακανόνιστων λεπτομερειών ή σχηματισμών συμβαίνει προοδευτικά σε μικρότερες κλίμακες και είναι δυνατόν να συνεχιστεί απεριόριστα έτσι ώστε κάθε τμήμα ενός τμήματος, όταν μεγεθυνθεί, να μοιάζει με το αρχικό σχήμα.
να χαρακτηριστικό τους ότι είναι όμοια προς εαυτόν. Έτσι αν κοιτάξουμε ένα μικρό τμήμα ενός fractal θα δούμε πως είναι όμοιο με ένα μεγαλύτερο τμήμα. Αν μεγεθύνουμε το μικρό, θα δούμε πως αυτό περιέχει και πάλι όμοια μέρη κ.ο.κ. Αυτή τους η ιδιότητα ονομάζεται αυτοομοιότητα. Αυτοόμοιο είναι ένα αντικείμενο του οποίου τα μέρη από τα οποία αποτελείται μοιάζουν με το σύνολο. Αυτή η επανάληψη των ακανόνιστων λεπτομερειών ή σχηματισμών συμβαίνει προοδευτικά σε μικρότερες κλίμακες και είναι δυνατόν να συνεχιστεί απεριόριστα έτσι ώστε κάθε τμήμα ενός τμήματος, όταν μεγεθυνθεί, να μοιάζει με το αρχικό σχήμα.
Οι fractal εικόνες οπότε είναι ανεξάρτητες από κλίμακα μεγέθους. Αντίθετα με τα ευκλείδεια σχήματα, δεν έχουν ένα χαρακτηριστικό μέγεθος μέτρησης.
Χαρακτηριστικό απλό παράδειγμα είναι η νιφάδα του Koch που βλέπουμε στην αντίστοιχη εικόνα.
Χαρακτηριστικό ενός φράκταλ είναι η μαθηματική παράμετρος που ονομάζεται διάσταση-fractal:D.
Παραμένει σταθερό ανεξάρτητα με το πόσο πολύ θα μεγεθυνθεί το αντικείμενο ή υπό ποία γωνία θα παρατηρηθεί. Η διάσταση fractal εκφράζεται με έναν μη ακέραιο αριθμό, δηλαδή από ένα "κλάσμα", αντίθετα προς την ευκλείδεια γεωμετρία.
Στο παραπάνω παράδειγμα, η περίμετρος κάθε σχήματος αυξάνει σε σχέση με την περίμετρο τού αμέσως προηγουμένου σχήματος κατά τον λόγο 4 προς 3. Η διάσταση fractal D είναι η δύναμη στην οποία πρέπει να υψωθεί το 3 για να δώσει 4, δηλαδή 3D = 4 οπότε D= log4/log3=1,26.
Το μήκος της περιμέτρου τού fractal είναι 3l*(4/3)*(4/3).... δηλαδή άπειρο, αλλά περικλείει ένα πεπερασμένο εμβαδόν που είναι μικρότερο από το εμβαδόν τού περιγεγραμμένου κύκλου στο αρχικό τρίγωνο. Η διάσταση fractal D αποκαλύπτει ακριβώς τις λεπτές διαφορές και την πολυπλοκότητα ενός μη ευκλείδειου σχήματος.
Εφαρμογές Fractals
Η γεωμετρία fractal με τις έννοιες τής αυτοομοιότητας και τής μη ακέραιης διάστασης έχει εφαρμοστεί σε φυσικά συστήματα που δ είχνουν φαινομενικά τυχαία χαρακτηριστικά.
είχνουν φαινομενικά τυχαία χαρακτηριστικά.
Για παράδειγμα έχουν γίνει προσομοιώσεις fractal για να σχεδιαστεί η κατανομή σμηνών γαλαξιών στο Σύμπαν και για να μελετηθούν προβλήματα που σχετίζονται με την διαταραχή της ροής των ρευστών στα όρια επαφής με τα τοιχώματα όπου γίνεται τυρβώδης με συμπεριφορά ανεξέλεγκτη[5]. Η γεωμετρία fractal συνέβαλε πολύ στα γραφικά με ηλεκτρονικό υπολογιστή, όπου αλγόριθμοι fractal σχεδιάζουν σχήματα πολύπλοκων, εξαιρετικά ακανόνιστων φυσικών αντικειμένων, όπως είναι μορφολογικά ανώμαλα όρη και περίπλοκα συστήματα κλαδιών δέντρων αλλά και σκηνές πολύπλοκες με τυχαία και ακανόνιστη κίνηση μεγάλων ομάδων αντικειμένων.
Παράδειγμα Fractal
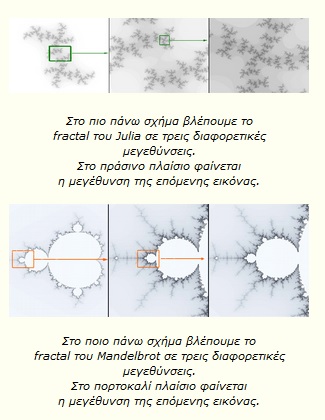 Τα σύνολα Julia (Από το όνομα του μαθηματικού Gaston Julia που τ' ανακάλυψε) δημιουργήθηκαν εισάγοντας ένα μιγαδικό αριθμό σε μια επαναληπτική συνάρτηση. Το σύνολο Mandelbrot προκύπτει από τα Julia και είναι το σύνολο όλων των δυνατών συνόλων Julia. Είναι από τα πιο φημισμένα fractal επειδή είναι εξαιρετικά σύνθετο και ήταν το πρώτο που ανακαλύφθηκε από τον ιδρυτή της fractal γεωμετρίας: τον Benoit Mandelbrot.
Τα σύνολα Julia (Από το όνομα του μαθηματικού Gaston Julia που τ' ανακάλυψε) δημιουργήθηκαν εισάγοντας ένα μιγαδικό αριθμό σε μια επαναληπτική συνάρτηση. Το σύνολο Mandelbrot προκύπτει από τα Julia και είναι το σύνολο όλων των δυνατών συνόλων Julia. Είναι από τα πιο φημισμένα fractal επειδή είναι εξαιρετικά σύνθετο και ήταν το πρώτο που ανακαλύφθηκε από τον ιδρυτή της fractal γεωμετρίας: τον Benoit Mandelbrot.
Ο τύπος για να τα σχεδιάσουμε στον υπολογιστή είναι Ζn+1=Z2n+K. Ο αλγόριθμος είναι ο εξής: Παίρνουμε ένα αριθμό z, τον πολλαπλασιάζουμε στον εαυτό του και τον προσθέτουμε στην σταθερά Κ. Εξετάζουμε αν η σειρά από τα σημεία που προκύπτουν έχει όλους της τους όρους να περιέχονται σε κύκλο με ακτίνα ίση με δύο. Αν ναι, τότε o z ανήκει στο σύνολο Mandelbrot και θα παριστάνεται σαν μια μαύρη κουκίδα. Έτσι βρίσκονται ένα ένα τα σημεία που συνθέτουν το σύνολο Mandelbrot οπότε καθορίζεται το σχήμα της γραφικής του αναπαράστασης. Έχει την παράξενη ιδιότητα ένα τμήμα του να μοιάζει με ολόκληρο το fractal. Φτάνει να παραστήσουμε κάποιο απόσπασμα και καταλαβαίνουμε πως είναι το ολόκληρο σχήμα. Αλλά ποιο είναι το ολόκληρο; Αυτό που χωράει σε ένα χαρτί, σε ένα τεράστιο χαρτόνι ή που χωράει σε όλη την Αθήνα;
Αρχίζει λοιπόν το γενικό και το τοπικό να συγχέονται.
Θεωρητικοί του Χάους
Αμερικανός μετεωρολόγος ο Edward Lorenz, Ασχολήθηκε με ζητήματα καιρικών προγνώσεων. Όταν πέρασε στις αναπαραστάσεις των μαθηματικών εξισώσεων που χρησιμοποιούσε βρέθηκε μπροστά σε μία μορφή που έμοιαζε με καρναβαλίστικη μάσκα του ντόμινο βλέπε εικόνα σελ. 5. Κατάλαβε ότι υπήρχε μια κρυμμένη δομή μέσα στο χάος. Μια τάξη στην οποία υπάκουαν τα σύννεφα και οι άνεμοι.
Η δομή αυτή, η «παράξενη έλξη» προέρχεται από το γεγονός ότι η συμπεριφορά των συστημάτων του καιρού, των κυμάτων κλπ δεν είναι απολύτως τυχαία, αλλά συγκεκριμένα οροθετημένη. Είναι δηλαδή ένα χάος ελεγχόμενο - μια παράξενη κατάσταση ανάμεσα στο προβλεπόμενο και το τυχαίο.
Ο Ιλιά Πριγκοζίν από τους πιο σημαντικούς σύγχρονους επιστήμονες (χημικός – μαθηματικός) οδηγήθηκε σε αντίστοιχα συμπεράσματα. Διαπίστωσε ότι οι ζωντανοί οργανισμοί βρίσκουν εν τέλει τάξη και νόμο, ζώντας εξαιτίας και μέσα σε ένα κόσμο που τρεκλίζει. Διατύπωσε ότι αυτή η τάξη προκύπτει από χημικά συστήματα ανισόρροπα και πολύπλοκα - δηλαδή χαοτικά.
Ισχυρίστηκε ακόμη ότι οι αλαζονικές κλασικές επιστήμες καταρρίπτονται (το ωρολογιακό σύμπαν του Νεύτωνα, η έννοια της αντιστρεψιμότητας, η γραμμική συμπεριφορά των συστημάτων) κι ότι ασήμαντες επιδράσεις, που οι επιστήμονες ως τώρα θεωρούσαν αμελητέες, μπορεί να εισχωρήσουν στο εσωτερικό των συστημάτων προκαλώντας, γιγαντιαίες αλλαγές, την ώρα που γιγαντιαίες δυνάμεις μπορεί ν' αφήνουν τα συστήματα ανέπαφα.
Το φτερούγισμα μιας πεταλούδας στην Αθήνα μπορεί λοιπόν να προκαλέσει καταιγίδα στο Τόκιο - αλλά το θέμα δεν είναι αυτό. Είναι ότι με τις νέες θεωρίες, ο άνθρωπος φτάνει στο σημείο να συνειδητοποιήσει ότι η έννοια του ελέγχου με την επιβολή ισχύος είναι ψευδαίσθηση. Η εντύπωση ότι η φύση ελέγχεται μέσω δύναμης είναι μια πλάνη. Η καθοδήγηση των μαζών; Η στάση-πράξη του ενός μπορεί να είναι αίτιο πρόκλησης παράξενου ελκυσμού;
Τώρα όλα μπορούν να ειδωθούν ως χάος. Χάνονται και ξαναβρίσκονται καινούρια. Η πορεία του κόσμου δεν είναι μια προβλέψιμη κίνηση, αλλά μια τεθλασμένη γραμμή που διαρκώς λυγίζει από το τυχαίο και δεν μπορεί ποτέ να γυρίσει προς τα ασφαλή μετόπισθεν. Είναι ένα ποτάμι χωρίς επιστροφή. Ο Ηράκλειτος επιβεβαιώνεται επιστημονικά σε βάθος.
Η μεταφορά της θεωρίας του χάους απαιτεί μεγάλη προσοχή. Δεν είναι πανάκεια που θεωρεί αυταπόδεικτη κάθε έλλειψη τάξης ούτε και λειτουργεί ηθικολογικά εναντίων του ελέγχου. Τουναντίον, η θεωρία του χάους έχει φτιαχτεί για να επιτευχθεί ακόμη μεγαλύτερος έλεγχος πάνω σε κάθε λογής συστήματα. Κατάφερε όμως να μας εξελίξει συνειδησιακά. Μας έδωσε την δυνατότητα να αντιληφθούμε με επιστημονικό τρόπο την ροϊκότητα των πραγμάτων και να συνειδητοποιήσουμε την σημαντικότητα των μικρών τοπικών επιρροών σε καθολικά συστήματα. Έτσι κάθε μικρή δράση αποκτά μεγάλη σημασία και μπορεί κανείς να ισχυριστεί ότι η ευθύνη περνά σε μεγαλύτερο βαθμό στην ατομική πράξη από ότι φανταζόμασταν παλαιότερα[6].
Κοντά στη θεωρία του χάους στέκει η θεωρία των καταστροφών του Rene Thom. Αυτή ψάχνει μια μαθηματική νομοτέλεια που κρύβεται πολλές φορές πίσω από κάθε βιολογική αλλαγή. Σκοπός, να εξηγήσει τις ξαφνικές αστάθειες σε σχετικά σταθερά συστήματα. Το γιατί π.χ. συμβαίνουν σεισμοί, ή γιατί αλλάζει το σχήμα ενός σύννεφου.
Η λέξη καταστροφή, δεν είναι κυριολεκτική. Μιλάει για εκείνη την απειροελάχιστη στιγμή όπου όλα παίζονται κι η αλλαγή συντελείται.
Ο Thom παρατήρησε κάτι που βρίσκουμε στην Ηρακλείτεια φιλοσοφία. Η εξέλιξη του κόσμου γίνεται μέσα από τις αλλαγές της μορφής. Μόνο που η διαδοχή αυτών των μορφών χαρακτηρίζεται από ασυνέχεια, από φάσεις δηλαδή όπου η αλλαγή συντελείται απότομα. Οι συνεχιστές της θεωρίας αυτής την γενίκευσαν σε ό,τι κινείται και παρουσιάζει ταυτόχρονα απότομες αλλαγές. Π.χ. στην γέννηση των βιολογικών μορφών (κύτταρα), στις κοινωνικές αλλαγές- επαναστάσεις, σε στασιασμούς κρατουμένων, στην πτώση καθεστώτων, ακόμη και ψυχολογικές συμπεριφορές που εμφανίζουν απότομες ψυχολογικές κρίσεις και μεταπτώσεις. Στην θεωρία αυτή όλα γίνονται αντικείμενο μελέτης με μαθηματικά εργαλεία.
Ιδρυτής της θεωρίας του χάους θεωρείται ο Γάλλος μαθηματικός της ΙΒΜ Μπενουά Μαντελμπρό. Αυτός εφεύρε πριν 25 χρόνια την μορφοκλασματική γεωμετρία (Fractal geometry), η οποία δίπλα στις καθαρές και συγκεκριμένες γραμμές της ευκλείδειας γεωμετρίας, εισάγει την έννοια της κλασματικής διάστασης που μας επιτρέπει να μετρήσουμε την αταξία, και το ακανόνιστο ενός αντικειμένου.
Είναι μια γεωμετρία, που μπορεί να αναπαραστήσει τις ατέλειωτες αντιθέσεις και στρεβλώσεις των φυσικών μορφών (της πλαγιάς ενός ηφαιστείου, του φύλλου μιας φτέρης, του πνεύμονα ενός εμβρύου κοκ) στην οθόνη ενός υπολογιστή.
Η πιο γνωστή εφαρμογή της μορφοκλασματικής γεωμετρίας έγινε από τον ίδιο. Ονομάζεται Mandelbrot Set και είναι μια μορφοκλασματική εικόνα που δημιουργείται σε υπολογιστή. Όσο κι αν μεγεθυνθεί, τόσο πιο σύνθετα και ψυχεδελικά σύμπαντα θα αποκαλύπτεί, το ίδιο άτακτα όπως η αρχική εικόνα, το ίδιο ανεξάντλητα εξίσου όμορφα.
Η θεωρία του χάους δεν είναι απλή. Στρέφει την επιστήμη σε ένα καινούριο δρόμο, πιο συμφιλιωμένο με την πραγματικότητα και συμφιλιώνει τον άνθρωπο με τον μέσα και έξω του Κόσμο καθιστώντας τον μια πιο υπεύθυνη οντότητα.
Γιατί και η καρδιά είναι ένα χαοτικό σύστημα. Χτυπάει ανεξέλεγκτα, τυφλά - κι όμως υπακούει κι αυτή σε ένα μαθηματικό νόμο.
Ποιον; Το νόμο του χάους. Τη γνώση της ελεγχόμενης αταξίας: Τη γνώση ότι το μάταιο σκόρπισμα, το διαρκές ξέφτισμα της ζωής δεν είναι εν τέλει τόσο μάταιο, ούτε και τόσο εντροπικό. Όλα λοιπόν υπακούνε σε μια τάξη ίσως μια κρυφή τάξη για τα μάτια του αμύητου.
Η Πράξη σαν Δημιουργία και Κοινωνική Αλληλεπίδραση
Οι αναλογίες από την θεωρία του χάους μπορούν να τονίσουν σημαντικά χαρακτηριστικά τέχνης και δημιουργικότητας και της σημασίας τους για την εκάστοτε πολιτεία. Καθένας μπορεί να γίνει η αρχική συνθήκη που παρόλη την τοπική ισχύ μπορεί να επηρεάσει, να είναι συνυπεύθυνος για την εκτροπή του συνόλου σε μια νέα ισορροπία.
Στο τελευταίο κεφάλαιο του βιβλίου του Postmodern Condition (1984), ο Lyotard προβλέπει ότι η κοινωνία της πληροφορικής θα ενισχύσει την εξουσία των κυριάρχων ελίτ, μέσω της πρόσβασής στους πληροφοριακούς πόρους. Ο κίνδυνος αυτός δημιουργίας ενός κέντρου εξουσίας μπορεί να αντιμετωπισθεί με την ανάδυση και την ανάπτυξη μέσα στις φυσικομαθηματικές επιστήμες θεωριών όπως η γεωμετρία των φράκταλ, η κβαντομηχανική, η θεωρία των καταστροφών. Θα μας επιτρέψουν "να εξαπολύσουμε έναν πόλεμο εναντίον της ολικότητας, να γίνουμε μάρτυρες αυτού που δεν μπορεί να παρουσιασθεί, να ενεργοποιήσουμε τις διαφορές και να σώσουμε την τιμή του ονόματος" (σελ. 82).
Κάτι άλλο που επίσης φαίνεται να έχει πολύ ενδιαφέρον είναι οι απόψεις του Prigogine για μια συνεργατική και επικοινωνιακή συμπεριφορά μακριά από συνθήκες ισορροπίας. Στο βιβλίο τους Order Out of Chaos (1984) ο Prigogine και η Stengers διατυπώνουν: "Στην ισορροπία τα μόρια συμπεριφέρονται ως ουσιαστικά ανεξάρτητες οντότητες, αγνοούν το ένα τα άλλα. Θα μπορούσαμε να τα ονομάσουμε "υπνόνια," "υπνοβάτες"... Όμως, η μη ισορροπία τα ξυπνά και εισάγει κάποια συνοχή εντελώς ξένη προς την ισορροπία" (σελ. 180-81).
Έτσι, η συνεργατική διαλεκτική του Prigogine στοχεύει στην προοπτική της ανανέωσης της σχέσης του ανθρώπου με την φύση. Όπως το βλέπει ο Αργυρός (Argyros, 1991), "η εκδοχή του Prigogine της μετανεωτερικής επιστήμης δεν είναι η καλλιέργεια ασυνεχειών και παραδόξων αλλά ένας νέος διάλογος με τον φυσικό κόσμο που σέβεται και την ετερότητά του και την θεμελιώδη συνέχειά μας με αυτόν" (σελ. 235). Αισιόδοξο συμπέρασμα, υπάρχει όμως και μια απαισιόδοξη συνέπεια: "… οδηγεί και στην ελπίδα και στην απειλή: ελπίδα, γιατί ακόμη και οι μικρές διαταραχές μπορούν να αυξηθούν και να μεταβάλουν τη συνολική δομή. Με αποτέλεσμα, η ατομική δραστηριότητα να μην είναι καταδικασμένη να παραμένει ασήμαντη. Από την άλλη όμως μεριά, αυτό είναι και απειλή, αφού στο σύμπαν μας η ασφάλεια των σταθερών, διαρκών κανόνων φαίνεται να έχει φύγει για πάντα" (Prigogine & Stengers, 1984, σελ. 313).
Η επίκληση του Prigogine για μια ηθική υπευθυνότητα αντιπροσωπεύει μια θαρραλέα θέση μπροστά σε ένα μεταβαλλόμενο χαοτικό σύμπαν.
Αυτό αλλάζει την αντίληψη ευθύνης του ατόμου, ειδικά των ποιητών-δημιουργών που η δράση τους δημιουργεί διαρκώς αρχικές συνθήκες, πιθανούς παράξενους ελκυστές.
Μια έκφραση πράξης μπορεί να είναι η τοπική συνεργατική, επικοινωνιακή συμπεριφορά που διαμορφώνει κατάλληλες αρχικές συνθήκες ώστε να επηρεάζει το σύνολο.
Μια άλλη περίπτωση είναι ότι αφού κάθε πράξη επιδρά σαν ένα κύμα στην επιφάνεια μιας ήρεμης λίμνης, τότε η συνειδητή πρόθεση του δημιουργού που συνυφαίνεται στο έργο επιδρά και δημιουργεί θεατές συμμέτοχους στην πρόθεση αυτή, ακόμη κι αν προκύπτει διαφωνία.
Σε κάθε περίπτωση όταν στην εκάστοτε πράξη συγκεραίνεται συνειδητή πρόθεση αυτό αναπτύσσει υπολογίσιμο βαθμό συμμετοχής στην δημιουργία του Κόσμου.
Αυτά τα στοιχεία περιέχονται στο κίνημα fluxus. Το ερώτημα είναι μήπως ένα τέτοιο σκεπτικό είναι παρωχημένο; Ποτέ η πράξη ενός ανθρώπου δεν μπορεί να είναι παρωχημένη. Ίσως είναι παρωχημένη η κινηματική μορφή δράσης του fluxus, αλλά η διαπίστωση ότι το είναι συμμετέχει σημαντικά διαμορφώνοντας κατάσταση πραγμάτων δεν έχει νόημα να αξιολογηθεί ως παρωχημένο.
Η θεωρία του χάους είναι ένα υπόβαθρο επιστημονικό πάνω στο οποίο μπορεί να θεμελιωθεί η αισιοδοξία ότι η ατομική δραστηριότητα είναι σημαντική.
Παρόλο που η θεωρία του χάους δημιουργήθηκε για να επιτευχθεί έλεγχος σε συστήματα που παρουσίαζαν ανεξέλεγκτη συμπεριφορά, τα αποτελέσματά της σε σχέση με τον έλεγχο αποκαλύπτουν μια καινούρια πτυχή στην έννοια του ελέγχου. Φανερώνεται ότι δεν μπορεί να υπάρξει έλεγχος σε απόλυτο βαθμό πουθενά. Η αντίληψη του τι είναι έλεγχος μετουσιώνεται. Η θεωρία του χάους προτείνει μια πιο ευέλικτη στάση, σύμπλευση με τις φυσικές διαδικασίες, σεβασμό στην αξία του τοπικού και του αμελητέου. Ανοίγει πύλη στην αλληλεπίδραση στοιχείου, συνόλου. Εξισορροπεί την ακόρεστη ανάγκη για καθολικό έλεγχο. Προτείνει, θα μπορούσε να διακινδυνέψει κανείς την άποψη, μια πιο ζεν άποψη για την ζωή.
Όλη αυτή η δομή σκέψης και πράξης επιδρά στην αντίληψη περί ελευθερίας. Η έννοια της ελευθερίας σε συνδυασμό με την αντίστοιχη υπευθυνότητα διευρύνεται. Το άτομο μπορεί να νιώσει πιο ελεύθερο, αφού πιστεύει ότι με την πράξη του, με το είναι του συμμετέχει στην διαμόρφωση της πραγματικότητας. Από την άλλη μπορεί να επωμισθεί την ευθύνη της υπόστασής του, της ύπαρξής του απέναντι στην ζωή και το σύνολο.
Αυτές οι σκέψεις είναι άξιες να μας επηρεάσουν. Μπορούν να αλλάξουνε την στάση μας και να βελτιώσουν την πράξη μας. Η τέχνη της μεταμόρφωσης του εαυτού ώστε να μπορεί να συνεισφέρει στο κοινό καλό είναι μια επίπονη αλλά πολύ ελκυστική διεργασία. Τίποτε από όλα αυτά δεν αποδεικνύεται. Είναι αξιωματικές και αυθαίρετες σκέψεις με περιεχόμενο πίστης που εμπνέονται από την θεωρία του χάους. Δίνουν χρηστική ερμηνεία στην κοινωνική-συνειδησιακή μεταφορά του χάους.
Καλλιτεχνική Δημιουργία και Χάος
Από την φ ύση της η θεωρία του χάους σχετίζεται με πολύ εντυπωσιακές εικόνες. Αυτό αναμφίβολα επηρεάζει τους καλλιτέχνες. Όμως ο λόγος που είναι σημαντική η ανίχνευση της επίδρασης της θεωρίας του χάους στην τέχνη είναι βαθύτερος. Αφενός η θεωρία του χάους άπτεται της θεωρίας της δημιουργίας καταστάσεων. Αυτό το ποιητικό αίτιο ενδιαφέρει πολύ την τέχνη. Αφετέρου η τέχνη πάντα είναι ο πρόσκοπος των κοινωνικών και συνειδησιακών αλλαγών. Αφουγκράζεται την αιχμή της επιστημονικής και φιλοσοφικής σκέψης με αντένες απλωμένες στο μέλλον και συνάμα βυθίζεται στα μύχια της ψυχής διεργασιών με έναν τρόπο υπερβατικό που μόνο στα θρησκευτικά πεδία μπορούμε να συναντήσουμε. Έτσι παρατηρώντας την ποιητική δράση των καλλιτεχνών, μπορούμε να εντοπίσουμε επόμενα εξελικτικά σκαλοπάτια της ανθρωπότητας. Στην ανίχνευσή της επίδρασης της θεωρίας του χάους σε καλλιτέχνες αλλά και στην αναζήτηση έργων που έχουν χαοτικό χαρακτήρα εντόπιξονται περιπτώσεις που έχει ενδιαφέρον να αναφερθούν.
ύση της η θεωρία του χάους σχετίζεται με πολύ εντυπωσιακές εικόνες. Αυτό αναμφίβολα επηρεάζει τους καλλιτέχνες. Όμως ο λόγος που είναι σημαντική η ανίχνευση της επίδρασης της θεωρίας του χάους στην τέχνη είναι βαθύτερος. Αφενός η θεωρία του χάους άπτεται της θεωρίας της δημιουργίας καταστάσεων. Αυτό το ποιητικό αίτιο ενδιαφέρει πολύ την τέχνη. Αφετέρου η τέχνη πάντα είναι ο πρόσκοπος των κοινωνικών και συνειδησιακών αλλαγών. Αφουγκράζεται την αιχμή της επιστημονικής και φιλοσοφικής σκέψης με αντένες απλωμένες στο μέλλον και συνάμα βυθίζεται στα μύχια της ψυχής διεργασιών με έναν τρόπο υπερβατικό που μόνο στα θρησκευτικά πεδία μπορούμε να συναντήσουμε. Έτσι παρατηρώντας την ποιητική δράση των καλλιτεχνών, μπορούμε να εντοπίσουμε επόμενα εξελικτικά σκαλοπάτια της ανθρωπότητας. Στην ανίχνευσή της επίδρασης της θεωρίας του χάους σε καλλιτέχνες αλλά και στην αναζήτηση έργων που έχουν χαοτικό χαρακτήρα εντόπιξονται περιπτώσεις που έχει ενδιαφέρον να αναφερθούν.
Ο Francis Bacon, πετώντας τυχαία χρώμα στο τελάρο, σε ένα προβληματικό σημείο του έργου, θεωρεί ότι το αποτέλεσμα που επιτυγχάνει το χρώμα από μόνο του είναι πολύ καλύτερο απ' αυτό που θα μπορούσε ο ίδιος να το οδηγήσει να κάνει. «Αυτό που σου δίνει το τυχαίο είναι τελείως διαφορετικό απ' αυτό που σου δίνει η συνειδητή επεξεργασία του χρώματος. Πολύ συχνά εμπεριέχεται στο τυχαίο ένα στοιχείο αναπόφευκτου, που δεν μπορεί να σου δώσει ο συνειδητός χειρισμός Το τυχαίο και ο έλεγχός του αλληλοσυμπληρώνονται, όντας τελείως διαφορετικές διεργασίες η μία από την άλλη[10].
Σημαντικότατο έργο στο οποίο το τυχαίο παίζει ρόλο είναι του Μαρσέλ Ντυσάν. Μια ιδιαίτερη περίπτωση δημιουργού, ο οποίος στήριξε το πνεύμα του Dada και αργότερα του σουρεαλισμού, αρνούμενος κάθε μορφή καλλιτεχνικής έκφρασης, και το έργο του οποίου χαρακτηρίζεται, όπως λέει και ο ίδιος, από την άρνηση της «οπτικής του αμφιβληστροειδούς». Με τις πράξεις του ως δημιουργός δεν θέλησε να επιβάλει μια νέα επαναστατική γλώσσα, αλλά να προτείνει μια πνευματική στάση.
Ο Ντυσάν χρησιμοποιεί το τυχαίο για λόγους καθαρά φιλοσοφικά ειρωνικούς, το χρησιμοποιεί σαν μέσον για να υπονομεύσει έναν λογικά κρατούμενο κόσμο. Κοροϊδεύει τον κόσμο στηριγμένο στη λογική, αρνούμενος την παντοδυναμία του καλλιτέχνη αποδέχεται το ρόλο της τύχης στη δημιουργία του έργου.
Στο Μεγάλο γυαλί, ο Ντυσάν άφησε τη σκόνη της Νέας Υόρκης να κατακαθίσει σ' ένα μέρος της κατασκευής. Στη συνέχεια ο Ντυσάν κόλλησε με ειδική ουσία τη σκόνη στη θέση της. Μ' αυτόν τον τρόπο ορισμένα μέρη του έργου πήραν μια κιτρινωπή απόχρωση, υπολογισμένη να τα ξεχωρίζει από το υπόλοιπο της σύνθεσης.
Όταν το Μεγάλο γυαλί ράγισε δεν το επιδιόρθωσε, αντίθετα δέχτηκε αυτά τα σημάδια της τύχης που είχαν ενσωματωθεί στο έργο του σαν ένα τελικό φινίρισμα, που καθόρισε την αποπεράτωση του έργου (1923).
Ένας ακόμη πολύ σημαντικός καλλιτέχνης, φυσικός επιστήμονας και τελετουργός Σαμάνος που θέτει το ερώτημα των σχέσης επιστήμης, τέχνης, θρησκείας και επιχειρεί να αναπροσδιορίσει τις σχέσεις τους με στόχο την εξέλιξη της σύγχρονης κοινωνίας είναι ο Beuys. Ποια θα μπορούσε να είναι η σκέψη του Beuys για την ιδέα του χάους; Στο διαδίκτυο στον χώρο του Walker Art Center θα βρεί κανείς τα εξής: “Η εμμονή του Beuys για τα φαινόμενα μεταστοιχείωσης της ύλης και του πνεύματος και της μετουσίωσης ως Χριστιανικό περιεχόμενο επηρεάσθηκε από την επαφή του με τα γραπτά του ιδρυτή της ανθρωποσοφίας Rudolf Steiner. Ο Beuys είχε διαβάσει τα γραπτά του Steiner σε νεαρή ηλικία αλλά μετά τον Β Παγκόσμιο πόλεμο απορροφήθηκε πλήρως σε βαθιά μελέτη τους. Οι θεωρίες του Steiner σχετικά με τις κοινωνικές σχέσεις, την εκπαίδευση και τον Χριστιανισμό αναμείχθηκαν με το μεγάλο ενδιαφέρον του Beuys για τις θετικές επιστήμες και το αμείωτο ενδιαφέρον του για την πνευματική και κοινωνική οργάνωση”[11].
Ο ιστορικός τέχνης John Moffitt ισχυρίζεται ότι κατά το μεγαλύτερο μέρος η δουλειά του Beuys και η προβολή του ως σαμάνου είναι πλήρως εμπνευσμένη από τις θεωρίες του R. Steiner[12].
Είναι διαφωτιστικό να συγκρίνει κανείς δύο κείμενα, ένα γραμμένο από τον Steiner to 1909 και ένα άλλο από τον Beuys το 1978.
Steiner: “Στην παρούσα εποχή της υλιστικής σκέψης, η εισροή πνευματικής γνώσης στον πολιτισμό μας είναι απαραίτητη για την ανθρωπότητα που διψάει για την γνώση αυτή… Ο μοντέρνος τρόπος σκέψης είναι απλώς αδύνατον να διαχειριστεί και να αντιληφθεί το χάος των εξωτερικών συνθηκών… Η ίδια η σκέψη θα γίνει άκαμπτή και σύντομα θα χάσει την ρευστότητα και την ευελιξία της ώστε να συλλάβει την πολυπλοκότητα των συνθηκών της ζωής και να μεταμορφωθεί μαζί τους… Το βαθύτερο νόημα του ρητού ΓΝΩΘΙΣΑΥΤΟ είναι η ικανότητά μας να ακολουθήσουμε την εξέλιξη του Κόσμου. Ο εαυτός είναι γεννημένος από το σύμπαν και η ίδια μας η εξέλιξη, μας οδηγεί να ενωθούμε τελικά με το όλον. Ο στόχος της αυτογνωσίας είναι να δώσει στον άνθρωπο την θέση στον Κόσμο, από όπου θα του αποκαλύψει την πραγματική έννοια του ρητού ΓΝΩΘΙ ΣΑΥΤΟ”[13].
Beuys: Όταν εκλαμβάνουμε την ίδια μας την υλιστική κατάστασή και τα βιώματα μας στην παρούσα κρίση ως αρνητικά, πρέπει συνάμα να λάβουμε υπόψη ότι αυτή η κατάσταση είναι επίσης και μια ιστορική αναγκαιότητα. Το βίωσα στον πόλεμο και το νιώθω και τώρα καθημερινά: Αυτή η παρακμή συνοδεύει την μονόθωρη κατανόηση του υλισμού. Όταν οι άνθρωποι λένε ότι η σαμανιστική πρακτική είναι μη ορθολογιστική και αταβιστική θα μπορούσε κανείς να απαντήσει ότι η στάση των σύγχρονων επιστημόνων είναι εξίσου παλιομοδίτικη και αταβιστική επειδή θα έπρεπε ήδη να βρισκόμαστε σε ένα άλλο στάδιο εξέλιξης στην σχέση μας με την ύλη. Έτσι όταν εμφανίζομαι ως μια σαμανιστική μορφή το κάνω για να τονίσω την πίστη μου σε άλλες προτεραιότητες και την ανάγκη να επανέλθουμε με ένα τελείως διαφορετικό τρόπο προσέγγισης των πραγμάτων. Για παράδειγμα σε μέρη όπως τα πανεπιστήμια, όπου όλοι μιλούν τόσο ορθολογιστικά, είναι απαραίτητο να εμφανιστεί κάποιο είδος μαγείας[13].
“Ο J. Cage προβληματίζεται σχετικά με τις έννοιες του τυχαίου και του ακαθόριστου, που τα θεωρεί σαν τους πραγματικούς δημιουργούς ενός έργου, που θα 'ναι πάντα καινούριο. Συνδέεται άμεσα με την ιδέα της Αλεατορικής μουσικής (aleatory music, από το λατινικό alea = κύβος, ζάρι), μια από τις τάσεις της μουσικής πρωτοπορίας μετά τον Β΄ Παγκόσμιο πόλεμο, όπου ο συνθέτης εισάγει στοιχεία τυχαία ή απρόβλεπτα – στη σύνθεση καθ' εαυτή, στην εκτέλεση, ή και στα δύο.
Στην «Μουσική των Αλλαγών» του Cage, για πιάνο, (1951) τα τονικά ύψη ορίζονται με ακρίβεια, οι διάρκειες όμως και η συχνότητα με την οποία επανέρχονται, υπαγορεύονται από το i-ching[14].
Στις ΗΠΑ συνδεμένοι με το κίνημα Fluxus[15] οι George Brecht και Jackson Mac Low διερευνούν τις διαφορετικές δυνατότητες του ακαθόριστου. Όπως ο Cage έτσι και ο Brecht πραγματοποιεί την «μουσικολογική έρευνα» του, θεωρώντας ότι όλες οι τυχαίες ακουστικές και οπτικές στιγμές κατά τη διάρκεια της συναυλίας ανήκουν στην υλοποίηση της παρτιτούρας.
To “Zen for film” (1962-64) του Nam June Paik, μια πρότυπη ταινία fluxus, παρουσιάστηκε στο fluxhall[16]. Η ταινία δεν ήταν παρά 1000 πόδια άγραφου φιλμ που προβαλλόταν ανεπεξέργαστο στην οθόνη για 30 λεπτά.
Η ταινία του Paik είναι χωρίς εικόνα ή ήχο και σε κάθε προβολή, γρατσουνιές, σκόνη και άλλα τυχαία συμβάντα εμφανίζονται αναπόφευκτα, το φιλμ είναι κατά κάποιο τρόπο κάθε φορά καινούριο.
 Παρόλο που ο Andy Goldsworthy δεν αναφέρεται στην θεωρία του χάους, αν προσέξει κανείς τα στοιχεία που τον ενδιαφέρουν και τον τρόπο με τον οποίο δουλεύει καταλαβαίνει ότι όλο του το έργο έχει συνάφεια με την λειτουργία της φύσης την εντροπία και τις μορφοκλασματικές δομές. Επιπλέον ο τρόπος που αντιμετωπίζει το προϊόν έργο και η διαδικασία εργασίας του σημαίνει σαφώς την ανίχνευση και σύμπλευσή του με την ροή των πραγμάτων.
Παρόλο που ο Andy Goldsworthy δεν αναφέρεται στην θεωρία του χάους, αν προσέξει κανείς τα στοιχεία που τον ενδιαφέρουν και τον τρόπο με τον οποίο δουλεύει καταλαβαίνει ότι όλο του το έργο έχει συνάφεια με την λειτουργία της φύσης την εντροπία και τις μορφοκλασματικές δομές. Επιπλέον ο τρόπος που αντιμετωπίζει το προϊόν έργο και η διαδικασία εργασίας του σημαίνει σαφώς την ανίχνευση και σύμπλευσή του με την ροή των πραγμάτων.
«Παίρνω τις ευκαιρίες που η κάθε μέρα μου προσφέρει. Όταν χιονίζει εργάζομαι με το χιόνι. Το φθινόπωρο, υλικό μου γίνονται τα φύλλα που πέφτουν. Σταματώ σε ένα μέρος ή σηκώνω ένα υλικό επειδή νιώθω ότι υπάρχει εκεί κάτι για να ανακαλυφθεί. Εκεί είναι που αρχίζω να μαθαίνω. Όταν εργάζομαι με ένα φύλλο, πέτρα ή ραβδί δεν είναι απλά ένα υλικό αλλά ένα άνοιγμα στις διαδικασίες ζωής εντός και γύρω του. Εκεί που το αφήνω, αυτές οι διαδικασίες συνεχίζονται. Η κίνηση, η αλλαγή, το φως, η δημιουργία και η διάλυση είναι το ρευστό της ζωής, το αίμα της φύσης. Είναι οι ενέργειες που προσπαθώ να διαχειριστώ με την δουλειά μου. Η φύση είναι σε κατάσταση διαρκούς αλλαγής και αυτή η αλλαγή είναι το κλειδί για την κατανόησή της. Ζητώ η τέχνη μου να είναι ευαίσθητη και εναργής σε αυτές τις αλλαγές των υλικών, των εποχών, του καιρού. Κάθε έργο αναπτύσσεται στέκει και κατόπιν διαλύεται. Η διαδικασία δημιουργίας και διάλυσης είναι αντίστοιχες»[17].
Επίδραση της Θεωρίας του Χάους στην Συνείδηση
Ο έλεγχος
Η επίδραση των θεωριών του χάους για κάποιον πρόθυμο να τις κάνει πράξη μπορεί ν α είναι καθοριστική. Ζούμε σε έναν κόσμο που δεσπόζουσα νοοτροπία είναι αυτή του έλεγχου. Ο έλεγχος επιχειρείται από τον άνθρωπο στην φύση, από ισχυρά κράτη με σκοπό την πλανητική κυριαρχία, από ισχυρές κοινωνικές ομάδες για οικονομική παντοδυναμία, από άνθρωπο σε άνθρωπο ανταγωνιστικά για διαπροσωπική εξουσία, από τον καθένα μας στον ίδιο του τον εαυτό με σκοπό την προσαρμογή σε ένα σύστημα αξιών που η δύναμη αποθεώνεται. Η λατρεία της δύναμης και του ελέγχου σε κάποιες περιπτώσεις έχει πάρει μορφή ομαδικής υστερίας. Το νιώθει κανείς σε κάθε έκφραση δημόσιου λόγου. Το βλέπει με την μορφή του τρομοκυνηγητού, με τις κάμερες που παρακολουθούν κάθε κίνηση στους δρόμους, με τον τρόπο που στήνονται τα δελτία ειδήσεων, με τους προσανατολισμούς και τα βαθύτερα αιτία τους που ο καθένας μας θέτει.
α είναι καθοριστική. Ζούμε σε έναν κόσμο που δεσπόζουσα νοοτροπία είναι αυτή του έλεγχου. Ο έλεγχος επιχειρείται από τον άνθρωπο στην φύση, από ισχυρά κράτη με σκοπό την πλανητική κυριαρχία, από ισχυρές κοινωνικές ομάδες για οικονομική παντοδυναμία, από άνθρωπο σε άνθρωπο ανταγωνιστικά για διαπροσωπική εξουσία, από τον καθένα μας στον ίδιο του τον εαυτό με σκοπό την προσαρμογή σε ένα σύστημα αξιών που η δύναμη αποθεώνεται. Η λατρεία της δύναμης και του ελέγχου σε κάποιες περιπτώσεις έχει πάρει μορφή ομαδικής υστερίας. Το νιώθει κανείς σε κάθε έκφραση δημόσιου λόγου. Το βλέπει με την μορφή του τρομοκυνηγητού, με τις κάμερες που παρακολουθούν κάθε κίνηση στους δρόμους, με τον τρόπο που στήνονται τα δελτία ειδήσεων, με τους προσανατολισμούς και τα βαθύτερα αιτία τους που ο καθένας μας θέτει.
Η ισορροπία μεταξύ ελέγχου και σύμπλευσης με την ροή της ζωής είναι η πρώτη επίδραση της θεωρίας του χάους.
Η τάξη δεν απαξιώνεται. 'Aλλωστε είναι και η θεμελιώδης αρχή κάθε εκδηλωμένου συμβάντος. Η ισορροπία είναι ο σκοπός, Η αρμονία μεταξύ ροής και τάξης, ελέγχου και ανοίγματος στις λεπτές επιρροές του περιβάλλοντος. Ο κίνδυνος του ελέγχου, με την ανεξέλεγκτη θεοποιημένη φύση του είναι ορατός, σήμερα ίσως περισσότερο από ποτέ. Οι δυνάμεις επιβολής του δεν είχαν ποτέ μαζικότερη εμβέλεια. Ένα από τα σημαντικότερα κανάλια επιβολής τους είναι τα ΜΜΕ.
Το άνοιγμα σε κάθε μικρή επίδραση είναι η πρόταση που συστήνει η θεωρία του χάους. Αυτό για να συμβεί χρειάζεται να αποβληθεί το κρυφό άγχος, ο φωλιασμένος στην ψυχή φόβος που μας επιβάλλει να επιθυμούμε τον έλεγχο των πάντων.
Το άνοιγμα
Αυτό το άνοιγμα απαιτεί ευαισθησία ώστε να μπορεί κανείς να ακούει τις λεπτές επιδράσεις και να είναι δεκτικός να τις ακολουθήσει. Για να είναι κανείς δεκτικός προϋποτίθεται ένας βαθύς σεβασμός σε κάθε έκφραση, κάθε πρόταση, κάθε επιρροή όσο ποταπή ή ασήμαντη κι αν φαίνεται. Απαιτείται μια πραγματικά ουμανιστική πρόθεση που δεν περιορίζεται μόνο σε ανθρώπους αλλά σε κάθε επίδραση του περιβάλλοντος. Με έναν μαγικό τρόπο τότε νιώθει κανείς ότι όλο το σύμπαν συνωμοτεί ώστε να τον διδάξει, να τον οδηγήσει να έρθει σε πραγματική επικοινωνία μαζί του. Η επικοινωνία έτσι παίρνει ξανά την ουσιαστική της μορφή, γίνεται αμφίδρομη, δεν ακούνε μόνο τα αυτιά αλλά ολόκληρη η οντότητά. Βέβαια η αμφίδρομη φύση της επικοινωνίας σημαίνει επίσης εκφορά λόγου, πράξης προς το περιβάλλον. Έτσι σπάνε οι αναστολές και οι «σεμνότητες» και απελευθερώνεται η διάθεση εκδίπλωσης προς τα έξω. Μόνο που αυτή την φορά η συνειδητότητα και η υπευθυνότητα δίνουν στην εκφορά μια πρόθεση που σαφώς συμπεριλαμβάνει ηθική.
Μια ηθική που υπαγορεύεται από την ενωτική φύση του κόσμου. Θα μπορούσε να πει κανείς ότι σε αυτό το σημείο συναντιούνται οι βουδιστές μονάχοι που σκυμμένοι φτιάχνουν τις μαντάλες και ο Ηράκλειτος. Μοιάζει το χάος να είναι μια διεπιστημονική διαπίστωση που γεφυρώνει ανατολή με δύση.
Ο χρόνος
Η γνώση των διαδικασιών που στήνουμε σαν ικρίωμα για να χτίσουμε οποιοδήποτε προϊόν είναι σημαντική. Η συνείδηση για το ποιες είναι οι δυνάμεις που δημιουργούν και πως το κάνουν, είναι ένα εργαλείο πλοήγησης στο χαοτικό σύστημα της ζωής. Η παρατήρηση και η γνώση για το πως λειτουργούμε είναι ένα θέμα που δεν τελειώνει ποτέ. Συνέχεια μαθαίνουμε κάτι καινούριο. Ποιο είναι εκείνο το κρίσιμο ίσως και μικρό γεγονός που μας οδηγεί σε μια συγκεκριμένη πράξη; Για το πέταγμα της πεταλούδας που είναι υπεύθυνο για κάθε τυφώνα που μας συμβαίνει θα πρέπει να ανατρέξουμε πίσω στον χρόνο. Να ανασκοπήσουμε την δράση μας. Αν από τον προβληματισμό αυτό δημιουργηθεί πράξη, ο απόηχός της πιθανόν να μας επηρεάζει καιρό.
Έτσι μπορούμε κάποτε να συνειδητοποιήσουμε ότι η πρόθεση με την οποία δρούμε διαρκώς, δημιουργεί συνέχεια «φράκταλ», αρχικές συνθήκες που παρόλη την ασημαντότητά τους μπορούν σαν ένα κύμα να καθιερώσουν νέα δεδομένα. Να δημιουργήσουν μια ροή που μπορούμε να ακολουθήσουμε με εμπιστοσύνη. Την εμπιστοσύνη στην ίδια την ζωή, και το θάυμα της μέσα στο οποίο συμμετέχουμε ενεργά.
Έτσι είναι φανερό ότι κάθε πράξη μπορεί να εκλαμβάνεται σαν ένα απόσπασμα της ζωής, ανήκει σε αυτήν. Έτσι δεν μπορεί να έχει συγκεκριμένη αρχή και τέλος χρονικά. Διαχέεται απλώνεται, αλλού βαθαίνει και αλλού επιδρά σε μεγάλο βαθμό.
Η διαδικασία και το προϊόν
Κάθε προϊόν προϋποθέτει διαδικασίες για την παραγωγή του. Μόλις όμως ολοκληρωθεί το προϊόν οι διαδικασίες που συνήθως δεν καταγράφονται χάνονται, μένουν στο παρασκήνιο. Παρόλα αυτά συχνά πυκνά ακούγεται ο «δρόμος» είναι που έχει αξία και όχι το αποτέλεσμα. Λέγοντας δρόμο-διαδρομή βέβαια εννοείται ακριβώς η διαδικασίες που αναπτύσσονται για την παραγωγή του προϊόντος. Έτσι, όλη η πρόθεση, όλη η συλλογιστική και ο προβληματισμός που στήνονται δυναμικά και διαλεκτικά για να παραχθεί το προϊόν γίνονται ασήμαντα και αόρατα για κάποιον που βλέπει μόνο το αποτέλεσμα. Το ερώτημα είναι: θα μπορούσε η ίδια η διαδικασία να είναι το σώμα της ζωής και όχι το προϊόν, το αποτέλεσμα, ο στόχος;
Η αισθητική
Η αισθητική δεν έχει μόνο θεωρητική σημασία. Η αισθητική αξία κάθε πράξης σχετίζεται με το κατά πόσο μια π΄ραξη μπορέι να χαρακτηριστεί ωραία ή άσχημα. Σχετίζεται με τις εκάστοτε συνθήκες, με την ηθική μας στάση και τα κίνητρα.
Ο Αξελός εξηγώντας την άποψη του Ηράκλειτου για την αισθητική γράφει: «…μέσα στην φύση που η ενότητά της είναι η ενότητα των αντιθέτων αποκαλύπτεται και για τον Ηράκλειτο μια αρμονία «καλλιτεχνική». Η αρμονία είναι άλλοτε φανερή κι άλλοτε αφανής, κι έτσι διαφεύγει από την προσοχή των ανθρώπων που δεν ξέρουν να συλλαμβάνουν τα φαινόμενα σαν μέρη μιας όμορφης ολότητας.
...αφού ο Κόσμος περιέχει το κάθε τι που είναι, περιέχει κι εμάς, τίποτε δεν ξεφεύγει από το συμπαντικό ρυθμό του ακατάπαυστου γίγνεσθαι που κάνει αχώριστα τα αντίθετα που συγκρούονται….
Ο Ηράκλειτος συλλαμβάνει ποιητικά το κάθε τι που γίνεται μέσα στο κύλισμα του χρόνου. …Η ποίηση είναι το εσωτερικό κίνητρο της ανθρώπινης δραστηριότητας, εφόσον είναι αυτή που γεννά ολοένα καινούριες δημιουργίες, με αφετηρία τις παλιές σε όλη την διάρκεια του γίγνεσθαι. Η ηρακλειτική σκέψη και γλώσσα είναι και οι δύο υπέρτατα ποιητικές, γιατί δημιουργούν ένα όραμα που αγκαλιάζει το βαθύ νόημα των φαινομένων που εμφανίζονται στο εσωτερικό της αρμονικής τάξης του κόσμου.
...το χάος «είναι» η αντίθετη και συμπληρωματική όψη του κόσμου. Η διαλεκτική, που φέρνει σε επικοινωνία τη μορφή και το άμορφο, την οικοδόμηση και την καταστροφή, το θετικό και το αρνητικό, μπορεί να ανατρέπει τις προοπτικές και φέρνει μπροστά μας αυτό που υπάρχει κίνδυνος να τα εκμηδενίσει όλα. Η παρουσίαση αυτού του τεράστιου κίνδυνου μας χαρίζει μια τραγική χαρά. Γιατί η φωτιά μπορεί να γίνει πυρκαγιά και να πυρπολήσει τον κόσμο, αυτόν τον κόσμο που αν και είναι ο ωραιότερος, είναι σαν σωρός από σκουπίδια χυμένα στην τύχη(απ.124)»[17].
Στην εισαγωγή του κεφαλαίου για την συμμετρία του φυσικού νόμου ο νομπελίστας φυσικός Richard Feynman, με το ανατρεπτικό του ύφος γράφει: «Είναι εύκολο να καταλάβει κανείς πως΄ ένα σώμα μπορεί να είναι συμμετρικό. Πως, όμως, μπορεί να υπάρχει συμμετρία σε έναν φυσικό νόμο; Και βέβαια δεν μπορεί, όμως οι φυσικοί αρέσκονται να χρησιμοποιούν συνηθισμένες λέξεις αποδίδοντας τους διαφορετική σημασία από την καθιερωμένη. Στην περίπτωσή μας, νιώθουν για τους φυσικούς νόμους ένα συναίσθημα όμοιο με εκείνο που δημιουργεί η συμμετρία και αυτό το ονομάζουν συμμετρία των νόμων»[18],[19].
Αυτά τα δύο σημεία έχουν την δύναμη να ορίσουν έναν νέο άξονα πάνω στον οποίο μπορεί κανείς να σταθεί για να αντιμετωπίσει το ζήτημα της αισθητικής. Υπάρχει μια σχέση μεταξύ των μορφοκλασματικών εικόνων (fractal) που παράγουν οι εξισώσεις του χάους με τις ίδιες τις εξισώσεις. Οι μεν εικόνες φανερώνουν μια αρμονία οπτική, οι εξισώσεις περιέχουν εντός τους αυτήν την αρμονία. Από αυτή την αντιστοίχιση το fractal ως εικόνα με το fractal ως μαθηματικό τύπο, επεκτείνοντας μπορεί κανείς να σχηματίσει την νοητική εικόνα του fractal ως ιδέα, ως έννοια. Η διαλεκτική σύγκρουση των αντιθέτων κατά την αισθητική που παρουσιάζει ο Αξελός βρήκε το ζευγάρι του χάους και του ελέγχου.
Τελικά;
Κάθε άνθρωπος είναι ένας καλλιτέχνης. Κάθε πράξη έχει ηθικό, αισθητικό και ποιητικό νόημα. Κάθε πράξη είναι μια δράση που διαμορφώνει τον κόσμο μέσα στον οποίο υπάρχουμε. Ας φροντίσουμε να γίνουμε ελεύθεροι και παράξενοι ελκυστές ενός κόσμου που έρχεται και μπορούμε να κάνουμε καλύτερο.
Σημειώσεις
[1]. Ησίοδος Θεογονία 116-122 .
[2]. Ζαν Ρισπέν ελληνική Μυθολογία εκδόσεις τριήρης Αθήνα.
[3]. Αρκετά κατατοπιστικές, εκλαϊκευμένες και συνάμα τεκμηριωμένες λεπτομέρειες για το θέμα μπορεί να βρει κανείς στα βιβλία: Ian Stewart: Παίζει ο θεός ζάρια; Η επιστήμη του χάους. και Ivar Ekeland Το Χάος, που αναφέρονται στην βιβλιογραφία.
[4]. Στο βιβλίο Stewart, Ian. Οι μυστικοί αριθμοί, από το σχήμα της χιονονιφάδας στο σχήμα του σύμπαντος. Αθήνα: Τραυλός, 2003. υπάρχει μια πολύ καλή ανάλυση της fractal δομής με κατατοπιστική ποιοτική εικονογράφηση.
[5]. Στο βιβλίο του Theodor Schwenk Το ευαίσθητο χάος παρουσιάζεται εκτενώς η σχέση του χάους με μορφογεννητικές διαδικασίες του νερού που εμφανίζονται σε κάθε εκδήλωση της φύσης, από τα έμβια υδρόβια έως τις έρημους.
[6]. Μπουντουρίδη, Μωυσή, Α. Περιοδικό Νεύσις Αρ.τευχ. 5 ΧΑΟΣ ΚΑΙ ΚΡΙΤΙΚΗ ΘΕΩΡΙΑ, σελ.115-121. Αθήνα:1996.
[7]. Ο ίδιος έλεγε στην γυναίκα του “Όλη μου η έγνοια εστιάζεται στους ρυθμούς της φύσης.”
[8]. H. Rosenberg 1951.
[9]. Σε άρθρο του Scientific American Ιανουάριος 2004 ελλ. Έκδ. ο Richard P. Taylor κάνει μια ανάλυση των πινάκων του Pollok με την οποία αποδεικνύει ότι ο καλλιτέχνης είχε αναπτύξει μια τεχνική με την οποία δημιουργούσε έναν πυκνό φράκταλ ιστό. Καθώς η τεχνική του εξελισσόταν, η πολυπλοκότητα των φράκταλ μορφών αυξανόταν.
[10]. F. Bacon, συνέντευξη στον D. Sylvester 1974.
[11]. Walker Art Center: http://www.walkerart.org/beuys//beuysframe.html
[12]. John F. Moffitt, Occultism in Avant-Garde Art: The Case of Joseph Beuys (UMI Research Press Ann Arbor, Michigan, 1988), 109.
[13]. John F. Moffitt, Occultism in Avant-Garde Art: The Case of Joseph Beuys (UMI Research Press Ann Arbor, Michigan, 1988), 108-109.
[14]. Βιβλίο των Αλλαγών, αρχαίο κινέζικο κείμενο με οδηγίες για να επιλέγει κανείς μαντείες από τους συνδυασμούς τυχαίων αριθμών που πετυχαίνει ρίχνοντας νομίσματα.
[15]. Όρος που επινόησε ο Maciunas το 1961 από το flow – ροή.
[16]. Χώρος του Maciunas στην Canal Street της Νέας Υόρκης.
[17]. Από τον δικτυακό τόπο: cgee.hamline.edu/see/goldsworthy/see_an_andy.html
[18]. Αξελός, Κώστας. Ο Ηράκλειτος και η φιλοσοφία. Αθήνα: Εξάντας, 1976.
[19]. Feynman, Richard. Ο χαρακτήρας του φυσικού νόμου. Ηράκλειο: Πανεπιστημιακές εκδόσεις Κρήτης, 1990.
[20]. Στο βιβλίο του Ian Stewart, Οι μυστικοί αριθμοί, από το σχήμα της χιονονιφάδας στο σχήμα του σύμπαντος, αναφέρει στο κεφάλαιο η συμμετρία του φυσικού νόμου: «Ο Αλμπερτ Αινστάιν κατέστησε την συμμετρία θεμέλιο των βαθύτερων νόμων της φύσης. Η άποψή του είναι ότι η φυσική λειτουργεί με τον ίδιο τρόπο σε όλα τα σημεία, όλες τις χρονικές στιγμές.»
Βιβλιογραφία
• Argyros, Alexander J. A. "Blessed Rage of Order: Deconstruction, Evolution, and Chaos". Ann Arbor: The
University of Michigan Press, 1991.
• Baudrillard, Jean. Η έκσταση της επικοινωνίας. Αθήνα: Καρδαμίτσα, 1991.
• Campbell, Joseph. Ο ήρωας με τα χίλια πρόσωπα. Αθήνα: Ιάμβλιχος, 1990.
• Ekeland, Ivar. Το Χάος. Αθήνα: Τραυλός, 1998.
• Feynman, Richard. Ο χαρακτήρας του φυσικού νόμου. Ηράκλειο: Πανεπιστημιακές εκδόσεις Κρήτης, 1990.
• Hayles, N. Katherine. "Chaos as Orderly Disorder: Shifting Ground in Contemporary Literature and Science."
New Literary History 20 (2): 305-22. 1989.
• Hayles, N. Katherine. "Chaos Bound: Orderly Disorder in Contemporary Literature and Science". Ithaca:
Cornell University Press, 1990.
• Lee, Smolin. Τρεις δρόμοι προς την κβαντική βαρύτητα, η νέα αντίληψη για το χώρο, το χρόνο και το σύμπαν.
Αθήνα: Κάτοπτρο,2002.
• Lyotard, Jean-Francois. "The Postmodern Condition: A Report on Knowledge". Minneapolis: University of
Minnesota Press, 1984.
• Peat, David. Briggs, J. Μια αιρετική άποψη για το χάος στην καθημερινή μας ζωή. Αθήνα: Τραυλός, 2001.
• Prigogine, Ilya, and Isabelle Stengers. "Order Out of Chaos: Man's New Dialogue with Nature". New York:
Bantam Books, 1984.
• Prigogine, Ilya. "From Being To Becoming". New York: W. H. Freeman and Company, 1980.
• Schwenk, Theodor. Το ευαίσθητο χάος. Αθήνα: Θρόϊσμα (Fagotto), 2000.
• Stewart, Ian. Οι μυστικοί αριθμοί, από το σχήμα της χιονονιφάδας στο σχήμα του σύμπαντος. Αθήνα:
Τραυλός, 2003.
• Stewart, Ian. Παίζει ο θεός ζάρια; Η επιστήμη του χάους. Αθήνα: Τραυλός, 1998.
• Αξελός, Κώστας. Ο Ηράκλειτος και η φιλοσοφία. Αθήνα: Εξάντας, 1976.
• Ρισπέν, Ζαν. Ελληνική Μυθολογία. Αθήνα: Τριήρης.
• Σαρτρ, Ζαν, Πωλ. Το πρόβλημα της μεθόδου- μαρξισμός και υπαρξισμός. Αθήνα: Εξάντας, 1975.
Λ.Κ






